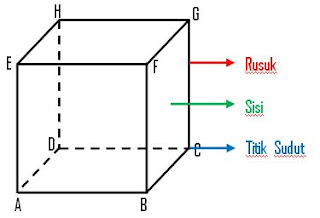
Biografi Pythagoras (580 - 475 M)
| Pencetus
sekaligus penguasa nisbah dan segitiga Pythagoras |
Apabila bilangan mengatur alam semesta, Bilangan adalah kuasa
yang diberikan kepada kita guna mendapatkan mahkota, untuk itu kita menguasai
bilangan. If “Number rules the universe, Number is merely our delegate to the
throne, for we rule Number.”
Pythagoras lahir di pulau Samos, Yunani selatan sekitar 580
SM (Sebelum Masehi). Dia sering melakukan perjalanan ke Babylon, Mesir dan
diperkirakan pernah sampai di India. Di Babylon, teristimewa, Pythagoras
menjalin hubungan dengan ahli-ahli matematika. Setelah lama menjelajah pulau
kecil, Pythagoras meninggalkan tanah kelahirannya dan pindah ke Crotona,
Italia. Diperkirakan Pythagoras sudah melihat 7 keajaiban dunia (kuno), dimana
salah satunya adalah kuil Hera yang terletak di kota kelahirannya. Sekarang,
kuil Hera sudah runtuh dan hanya tersisa 1 pilar yang tidak jauh dari kota
Pythagorian (namanya dipakai untuk mengenang putra terbaiknya). Menyeberangi selat
dan beberapa mil ke utara adalah Turki, terdapat keajaiban lain yaitu: Ephesus.

Pythagoras adalah anak Mnesarchus, seorang pedagang yang
berasal dari Tyre. Pada usia 18 tahun dia bertemu dengan Thales. Thales,
seorang kakek tua, mengenalkan matematika kepada Pythagoras lewat muridnya yang
bernama Anaximander, namun yang diakui oleh Pythagoras sebagai guru adalah
Pherekydes.
Pythagoras meninggalkan Samos pada tahun 518 SM. Tidak lama
kemudian dia membuka sekolah di Croton yang menerima murid tanpa membedakan
jenis kelamin. Sekolah itu menjadi sangat terkenal bahkan Pythagoras akhirnya
menikah dengan salah satu muridnya. Gambaran rinci tentang Pythagoras tidak
terlalu jelas. Dikatakan setelah itu, dia pergi ke Delos pada tahun 513 SM
untuk merawat penolong sekaligus gurunya, Pherekydes. Pythagoras menetap di
sana sampai dia meninggal pada tahun 475 SM. Sepeninggalnya, sekolah Croton
berjalan terseok-seok dan banyak konflik internal, tetapi dapat terus berjalan
sampai 500 SM sebelum menjadi alat politik.
Bagaimana
Pythagoras menciptakan kultus terhadap angka?
Angka adalah “dewa” Matematika dan “mitos-mitos” palsu
tentang angka tidak dapat dipisahkan. Setiap angka adalah simbol atau
melambangkan sesuatu yang terkait dengan metafisik adalah hal lumrah di Cina. Pythagoras
pun tidak luput dari “perangkap” mitos tentang angka. Dia mengajarkan bahwa:
angka satu untuk alasan, angka dua untuk opini, angka tiga untuk potensi, angka
empat untuk keadilan, angka lima untuk perkawinan, angka tujuh untuk rahasia
agar selalu sehat, angka delapan adalah rahasia perkawinan. Angka genap adalah
wanita dan angka ganjil/gasal adalah pria. “Berkatilah kami, angka dewa,”
adalah kutipan dari para pengikut Pythagoras yang memberi perlakuan khusus
terhadap angka empat,”yang menciptakan dewa-dewa dan manusia, O tetraktys suci
yang mengandung akar dan sumber penciptaan yang berasal dari luar manusia.
Pemujaan angka seperti layaknya tukang sihir dengan bola
kristalnya barangkali – di kemudian hari, mendasari para matematikawan setelah
Pythagoras. Ucapan Plato “Tuhan memahami geometri” atau kutipan Galileo “Buku
terbesar tentang alam ditulis dengan simbol-simbol matematika.” Apakah itu
termasuk ilmu sihir atau matematika. Yang jelas matematika lebih sulit untuk
dipahami.
Hubungan matematika dengan musik dekat sekali. Tidaklah
mengherankan apabila Pythagoras juga mampu menjadi seorang musisi. Mitos
bilangan Pythagoras terkandung lewat “keajabiban” pentagram. Bentuk segi-lima
yang makin lama makin kecil sampai takterhingga.
Pythagoras sebagai pemusik Pythagoras juga dikenal sebagai
musisi berbakat, seorang pemain lira. Penemuan musik terkait dengan matematika
diawali ketika Pythagoras bermain monokord, sebuah kotak dengan bentangan
tali-tali di atas salah satu sisinya. Dengan menggerakkan jari naik dan turun
pada garis-garis yang sengaja dibuat, Pythagoras mengenali bahwa suara yang
dihasilkan dapat diperkirakan. Ketika bagian tengah ditekan, setiap bagian atas
tali dan bawah tali menghasilkan nada sama: nada yang tepat 1 oktaf * lebih
tinggi dibandingkan apabila monokord tidak ditekan. Dengan membagi monokord
dengan nisbah 3/4 dan 2/5, ternyata setiap nisbah menghasilkan nada yang
berbeda, merdu atau fals. Baginya, harmoni musik adalah aktivitas matematika.
Harmoni dari monokord adalah harmoni matematika-dan harmoni alam semesta.
Pythagoras menyimpulkan bahwa nisbah tidak hanya berlaku pada musik tetapi juga
pada pelbagai jenis keindahan lain. Para pengikut Pythagoras menyimpulkan bahwa
nisbah dan proporsi mengendalikan keindahan musik, kecantikan fisik dan
keanggunan matematika.
Contoh: sebuah tali panjang yang menghasilkan nada C,
kemudian 16/15 dari panjang tali C menghasilkan notasi B; 6/5 panjang tali C
menghasilkan notasi A, 4/3 panjang tali C menghasilkan notasi G; 3/2 panjang
tali C menghasilkan notasi F; 8/5 panjang tali C menghasilkan notasi E; 16/9
panjang tali C menghasilkan notasi D dan 2/1 panjang tali C menghasilkan notasi
C rendah.
Penelitian tentang suara mencapai puncaknya pada abad 19
setelah John Fourier mampu membuktikan bahwa semua suara – instrumental maupun
vokal – dapat dijabarkan dengan matematika, yaitu jumlah fungsi-fungsi Sinus
sederhana. Menurutnya, suara mempunyai 3 kategori – pitch, loudness dan
quality. Penemuan Fourier ini memungkinkan ketiga kategori tersebut digambar
dan dibedakan. Pitch terkait dengan frekuensi kurva, loudness terkait dengan
amplitudu dan quality terkait dengan bentuk dari fungsi periodik. Lewat motto
“Angka adalah dewa”, Pythagoras mampu menggalang sejumlah pengikut.
Para pengikut Pythagoras (Pythagorean) Pythagoras barangkali
dapat disebut sebagai pemikir new ages pada jamannya. Dia juga seorang orator
ulung, intelektual terkenal sekaligus guru yang kharismatik. Semua itu membuat
banyak orang ingin belajar darinya. Tidaklah mengherankan apabila tidak lama
kemudian dia mempunyai banyak pengikut dan disusul dengan mendirikan sekolah.
Falsafah dasar yang paling penting bagi Pythagoras adalah:
angka. Yunani mewarisi pemahaman tentang angka dari geometrik Mesir. Hasilnya,
ahli matematika Yunani tidak dapat membedakan antara bentuk (shapes) dengan
bilangan (numbers). Pada saat ini untuk membuktikan theorema matematika biasa
digunakan gambar-gambar yang digambar dengan menggunakan sejenis penggaris yang
terbuat dari logam atau batu dan kompas.
Nisbah-nisbah adalah kunci untuk memahami alam, Pythagorean
dan matematikawan lebih modern menghabiskan banyak energi dengan menggali lebih
dalam teori-teori mereka. Akhirnya mereka memilah proporsi ke dalam sepuluh
kategori berbeda yang disebut dengan titik tengah harmonis (harmonic means).
Salah satu dari titik tengah ini mengandung angka paling “cantik” di dunia:
nisbah emas (golden ratio). Tidak ada yang istimewa dari nisbah emas ini,
tetapi sesuatu yang terinspirasi oleh nisbah emas tampaknya merupakan
obyek-obyek yang sangat indah. Bahkan sampai saat ini, artis dan arsitek secara
intuitif mengetahui bahwa obyek-obyek yang mengandung nisbah emas nampak
artistik. Dan nisbah ini mempengaruhi banyak pekerjaan pada bidang seni dan
arsitektur. Parthenon, kuil Athena terbesar, dibangun dengan kaidah nisbah emas
ada pada setiap aspek kontruksinya. Dalam pikiran Pythagorean, nisbah
mengendalikan alam semesta dan berarti sahih bagi seluruh dunia Barat pula.
Cacat
pada doktrin Pythagorean
Angka nol tidak mendapat tempat dalam kerangka kerja
Pythagorean. Angka nol tidak ada atau tidak dikenal dalam kamus Yunani.
Menggunakan angka nol dalam suatu nisbah tampaknya melanggar hukum alam. Suatu
nisbah menjadi tidak ada artinya karena “campur tangan” angka nol. Angka nol
dibagi suatu angka atau bilangan dapat menghancurkan logika. Nol membuat
“lubang” pada kaidah alam semesta versi Pythagorean, untuk alasan inilah
kehadiran angka nol tidak dapat ditolerir. Pythagorean juga tidak dapat
memecahkan “problem” dari konsep matematika – bilangan irrasional, yang
sebenarnya juga merupakan produk sampingan (by product) rumus: a² + b² = c².
Konsep ini juga menyerang sudut pandang mereka, namun dengan semangat
persaudaraan tetap dijaga sebagai sebuah rahasia. Rahasia ini harus tetap
dijaga jangan sampai bocor atau kultus mereka hancur. Mereka tidak mengetahui
bahwa bilangan irrasional adalah “bom waktu” bagi kerangka berpikir
matematikawan Yunani.
Nisbah antara dua angka tidak lebih dari membandingkan dua
garis dengan panjang berbeda. Anggapan dasar Pythagorean adalah segala sesuatu
yang masuk akal dalam alam semesta berkaitan dengan kerapian (neatness),
proporsi tanpa cacat atau rasional. Nisbah ditulis dalam bentuk a/b bilangan
utuh, seperti: 1, 2 atau 17, dimana b tidak boleh sama dengan nol karena dengan
itu akan menimbulkan bencana. Tidak perlu dijelaskan lagi, alam semesta tidak
sesuai dengan kaidah tersebut. Banyak angka tidak dapat dinyatakan semudah itu
ke dalam nisbah a/b. Kehadiran angka irrasional tidak dapat dihindari lagi
adalah konsekuensi matematikawan Yunani.
Persegi panjang adalah bentuk paling sederhana dalam
geometri, tetapi dibaliknya terkandung bilangan irrasional. Apabila anda
membuat garis diagonal pada persegi panjang – muncul irrasional, dan kelak
besarnya ditentukan oleh akar bilangan. Bilangan irrasional terjadi dan akan
selalu terjadi pada semua bentuk geometri. Contoh lain, segi tiga siku-siku
dengan panjang kedua sisi adalah satu, dapat dihitung panjang sisi lain –
dengan rumus Pythagoras, yaitu: v2. Sangatlah sulit menyembunyikan hal ini bagi
orang yang paham geometri dan nisbah.
Hippasus
menyangkal
Rahasia ini akhirnya dibocorkan oleh seorang pengikut
Pythagorean yang merasa bahwa dia harus mengungkapkan kebenaran. Hippasus
adalah matematikawan yang menjadi murid sekaligus pengikut Pythagoras. Hippasus
berasal dari Metapontan. Pengungkapan rahasia membuat dia dijatuhi hukuman
mati. Cerita tentang bagaimana meninggalnya Hipassus ada berbagai versi.
Beberapa mengatakan bahwa Hippasus ditenggelamkan di laut, sebagai konsekuensi
menghancurkan teori indah dengan fakta-fakta menyesatkan. Sumber lain
menyebutkan bahwa para pengikut Pythagoras mengubur dia hidup-hidup. Lainnya
menyebutkan bahwa Hippasus, dibuang atau diasingkan dalam ruangan tertutup
tanpa pernah bertemu orang lagi.
Tanpa usaha mengklarifikasikan mana yang benar, namun yang
jelas pengungkapan oleh Hippasus ini mengoncangkan fondasi-fondasi doktrin
Pythagoras. Dalam hal ini Pythagorean menanggap bahwa bilangan irrasional hanya
sebagai suatu perkecualian. Mereka tidak dapat membuktikan bahwa bilangan
irrasional mencemari pandangan mereka tentang alam semesta.
Meninggalnya
Pythagoras
Para pengikut Pythagoras menyatakan bahwa guru mereka
meninggal dengan cara yang unik. Beberapa dari mereka menyatakan Pythagoras mogok
makan, sebagian lagi menyatakan bahwa dia mengurung dan berdiam diri. Cerita
lain menyatakan bahwa konon rumahnya dibakar oleh para musuhnya (mereka yang
merasa tersingkirkan oleh kehadiran Pythagoras di tempat itu). Semua
pengikutnya ke luar dari rumah terbakar dan lagi ke segala penjuru untuk
menyelamatkan diri. Massa yang membakar rumah itu kemudian membantai para
pengikutnya (pythagorean) satu per satu. Persaudaraan sudah dihancurkan.
Pythagoras sendiri berusaha melarikan diri tetapi tertangkap dan dipukuli. Dia
disuruh berlari di suatu ladang, namun mengatakan bahwa dia lebih baik mati.
Kemudian diambil keputusan bersama dan diputuskan: Pythagoras dihukum pancung
di muka umum.
Meskipun persaudaraan sudah bubar dan pemimpinnya terbunuh,
esensi ajaran Pythagoras terus bertahan sampai sekarang. Falsafah Barat banyak
dipengaruhi oleh pemikiran Pythagoras – seperti halnya doktrin Aristoteles,
ternyata mampu bertahan hampir 2 milenium. Angka nol dan bilangan irrasional
bertentangan dengan doktrin tersebut, tetapi memberi landasan bagi para
matematikawan berikutnya agar memperhatikan angka nol dan bilangan irrasional.
*) Oktaf artinya 8 yaitu: nada dari 1(do) sampai 1 (do
tinggi) atau dari C sampai C lagi
Sumbangsih
Penemuan Pythagoras dalam bidang musik dan matematika tetap
hidup sampai saat ini. Theorema Pythagoras tetap diajarkan di sekolah-sekolah
dan digunakan untuk menghitung jarak suatu sisi segitiga. Sebelum Pythagoras
belum ada pembuktian atas asumsi-asumsi. Pythagoras adalah orang pertama yang mencetuskan
bahwa aksioma-aksioma, postulat-postulat perlu dijabarkan terlebih dahulu dalam
mengembangkan geometri.
Manfaat ini, kelak, membuat matematika tetap dapat digunakan
sebagai alat bantu dalam melakukan perhitungan terhadap pengamatan terhadap
fenomena-fenomena alam, setelah melalui pengembangan dan penyempurnaan oleh
para matematikawan setelah Pythagoras. Theorema Pythagoras mendasari adanya theorema
Fermat (tahun 1620): x2 + y2 = z2 yang baru
dapat dibuktikan oleh Sir Andrew Wiles pada tahun 1994.
Lihat Video Tutorial Excel "Menggunakan Fungsi Count If untuk mencari Jumlah Data Tertentu pada Ms Excel"