Luas Permukaan dan Volume Kubus

Kubus

Pernahkah kamu melihat dadu? Dadu merupakan salah satu alat permainan yang berbentuk kubus. Apa yang dimaksud dengan kubus?

1.     Definisi Kubus

Kubus adalah sebuah bangun ruang yang semua sisinya berbentuk persegi dan semua rusuknya sama panjang. Gambar di samping menunjukkan sebuah kubus ABCD.EFGH yang memiliki unsur-unsur sebagai berikut.

2.     Unsur-Unsur Kubus

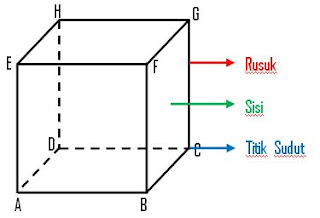
a.     Sisi/Bidang

Sisi kubus adalah bidang yang membatasi kubus. Kubus memiliki 6 buah sisi yang semuanya berbentuk persegi, yaitu ABCD (sisi bawah), EFGH (sisi atas), ABFE (sisi depan), CDHG (sisi belakang), BCGF (sisi samping kiri), dan ADHE (sisi samping kanan).

b.     Rusuk

Rusuk kubus adalah garis potong antara dua sisi bidang kubus dan terlihat seperti kerangka yang menyusun kubus. Coba perhatikan kembali Gambar Kubus ABCD.EFGH. Kubus memiliki 12 buah rusuk, yaitu AB, BC, CD, DA, EF, FG, GH, HE, AE, BF, CG, dan DH. Rusuk-rusuk yang sejajar pada kubus :  AB//DC//EF//HG ; AD// BC// FG//EH ; dan  AE// BF//CG// DH

c.     Titik Sudut

Titik sudut kubus adalah titik potong antara dua rusuk. Dari Gambar 8.2 , terlihat kubus ABCD. EFGH memiliki 8 buah titik sudut, yaitu titik A, B, C, D, E, F, G, dan H.

Selain ketiga unsur di atas, kubus juga memiliki diagonal. Diagonal pada kubus ada tiga, yaitu diagonal bidang, diagonal ruang, dan bidang diagonal.

a.     Diagonal Bidang

Coba kamu perhatikan kubus ABCD.EFGH. Pada kubus tersebut terdapat garis EG dan FH yang menghubungkan dua titik sudut yang saling berhadapan dalam satu sisi/bidang. Ruas garis tersebut dinamakan sebagai diagonal bidang. Kubus mempunyai 12 diagonal bidang, diantaranya adalah : AC, BD, FH, GE, BE, AF, DG, CH, BG, CF, AH, DE

b.     Diagonal Ruang

Kubus ABCD.EFGH disamping terdapat ruas garis HB dan EC yang menghubungkan dua titik sudut yang saling berhadapan dalam satu ruang. Ruas garis tersebut disebut diagonal ruang. Kubus mempunyai 4 diagonal ruang, diantaranya AG, HB,CE, dan DF.

c.     Bidang Diagonal

Perhatikan kubus ABCD.EFGH secara saksama. Pada gambar tersebut, terlihat dua buah diagonal bidang pada kubus ABCD. EFGH yaitu BD dan HF. Ternyata, diagonal bidang BD dan HF beserta dua rusuk kubus yang sejajar, yaitu BF dan DH membentuk suatu bidang di dalam ruang kubus bidang BDHF pada kubus tersebut.

Bidang diagonal adalah bidang yang dibatasi oleh dua rusuk dan dua diagonal bidang pada kubus. Kubus memiliki 6 bidang diagonal. Bidang diagonal kubus ABCDEFGH adalah : BDHF, ACGF, ABGH, CDEF, ADGF, BCHE

3.     Cara Melukis Kubus

Langkah-langkah melukis kubus :

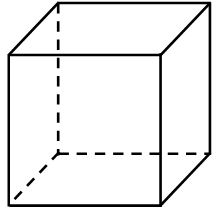
a.     Lukislah dua buah persegi, sebagai bagian sisi depan dan sisi belakang kubus. Rusuk yang tidak terlihat dari depan lukislah dengan garis putus-putus. 

b.     Hubungkan rusuk-rusuk dari depan ke belakang. Terbentuklah sebuah kubus.

4.     Sifat-Sifat Kubus

Untuk memahami sifat-sifat kubus, coba kamu perhatikan Gambar di samping. Gambar tersebut menunjukkan kubus ABCD.EFGH yang memiliki sifat-sifat sebagai berikut.

1.     Semua sisi kubus berbentuk persegi.

2.     Semua rusuk kubus berukuran sama panjang.

3.     Setiap diagonal bidang pada kubus memiliki ukuran yang sama panjang.

4.     Setiap diagonal ruang pada kubus memiliki ukuran sama panjang.

5.     Setiap bidang diagonal pada kubus memiliki bentuk persegipanjang.

5.     Kerangka Kubus

Sebuah kubus memiliki 12 rusuk. Jika panjang rusuk kubus adalah s maka jumlah panjang rusuknya adalah 12r.

6.     Jaring-Jaring Kubus

Jaring-jaring kubus ada 11 yaitu :

7.     Luas Permukaan Kubus

Misalkan, kamu ingin membuat kotak makanan berbentuk kubus dari sehelai karton. Jika kotak makanan yang diinginkan memiliki panjang rusuk 8 cm, berapa luas karton yang dibutuhkan untuk membuat kotak makanan tersebut? Masalah ini dapat diselesaikan dengan cara menghitung luas permukaan suatu kubus.

Luas permukaan kubus adalah jumlah luas sisi-sisi kubus. Kalian ingat bahwa kubus mempunyai 6 sisi dengan panjang rusuk (r). Sedangkan sisi kubus merupakan bangun datar yaitu persegi. Jadi, untuk mencari luas permukaan kubus adalah 6 kali luas persegi. Atau dengan rumus :

L _{permukaan kubus} = 6 × r²

8.     Volume Kubus

Misalkan, sebuah bak mandi yang berbentuk kubus memiliki panjang rusuk 1,2 m. Jika bak tersebut diisi penuh dengan air, berapakah volume air yang dapat ditampung? Untuk mencari solusi permasalahan ini, kamu hanya perlu menghitung volume bak mandi tersebut. Bagaimana mencari volume kubus? Masalah ini dapat diselesaikan dengan cara menghitung Volume suatu kubus. Perhatikan gambar dibawah ini.

Kubus di atas mempunyai 8 kubus kecil. Kubus-kubus kecil tersebut merupakan isi/volume kubus besar. Dengan kata lain, volume kubus di samping adalah 2 satuan x 2 satuan x 2 satuan = 8 satuan.

V _kubus = rusuk x rusuk x rusuk = r x r x r = r³

9.     Contoh Soal

a.     Sebuah bak air berbentuk kubus dengan alas berukuran 50 cm × 50 cm. Berapakah volume air yang harus diisikan pada bak tersebut agar dapat terisi sampai penuh?

Penyelesaian:

Diketahui:

r = 50 cm

Ditanyakan:

V _kubus = . . . .

Solusi:

V _kubus = r x r x r

         = 50 cm x 50 cm x 50 cm

         = 125.000 cm³

Jadi, banyaknya air yang harus diisikan pada bak tersebut adalah 125.000 cm³ atau 125 liter.

b.     Suatu kubus memiliki panjang rusuk 15 cm. Tentukan luas permukaan kubus tersebut?

Penyelesaian:

Diketahui:

r = 15 cm

Ditanyakan:

L _{permukaan kubus} = . . . .

Solusi:

L _{permukaan kubus} = 6 × r²

                     = 6 × 15²

                     = 6 × 15 cm × 15 cm

                     = 6 × 225 cm²

                     = 1350 cm²

Jadi, luas permukaan kubus tersebut adalah 1350 cm².