A. Momen
1. Momen
Jika X adlah peubah acak, baik diskrit
maupun kontinu, maka momen ke-k (dinotasikan dengan μ’k) didefinisikan sebagai:
μ’k = E(Xk),
k=1,2,3, ...
2. Momen Diskrit
Jika X adalah peubah acak diskrit dan p(x) adalah
nilai fungsi peluang dari X di x, maka momen ke-k ( dinotasikan dengan μ’k) didefinisikan sebagai:
Contoh:
Berikut
ini diberikan distribusi peluang dari peubah acak X.
Hitung
nilai μ’3
Penyelesaian :
Berdasarkan definisi momen diskrit, maka:
3. Momen Kontinu
Jika
X adalah peubah acak kontinu dan f(x) adalah nilai fungsi densitas dari X di x,
maka momen ke-k ( dinotasikan dengan μ’k) didefinisikan sebagai :
Contoh :
Misalnya
fungsi dnsitas dari X berbentuk:
Hitung μ’3
Penyelesaian :
B. Fungsi Pembangkit Momen
Pada
bagian sebelumnya, kita membahas momen ke-k
yang dinotasikan dengan μ’k. Momen ini bisa juga diperoleh melalui
besaran lainnya, yang dinamakan fungsi
pembangkit momen. Sehingga fungsi pembangkit momen merupakan sebuah fungsi yang
dapat menghasilkan momen-momen. Selain itu, penentuan distribusi baru dari
peubah acak yang baru merupakan kegunaan lain fungsi pembangkit momen.
1. Fungsi pembangkit Momen
Definisi
1
Jika X adalah peubah acak , baik dari
diskrit maupun kontinu, maka fungsi pembangkit momen dari X (dinotasikan dengan
(Mx(t)) didefinisikan sebagai:
Mx(t) = E(etX)
Untuk –h < t 0
2. Fungsi Pembangkit Momen Diskrit
Definisi
2
Jika
adalah peubah acak diskrit dan p(x) adalah nilai fungsi peluang dari X
di x, maka fungsi pembangkit momen dari X didefinisikan sebagai :
3. Fungsi Pembangkit Momen Kontinu
Definisi
3
Jika X adalah peubah acak kontinu dan f(x) adalah nilai
fungsi densitas dari X di x, maka fungsi pembangkit momen dari x didefinisikan
sebagai :
Berikut
ini akan dijelaskan dua cara dalam pembuktian bahwa fungsi pembangkit momen itu
bisa menghasilkan momen – momen.
1. Jika definisi 1, etX diuraikan dengan menggunakan perluasan deret
MacLaurin, maka dapat diperoleh :
Jika Mx(t) diturumkan terhadap t, kemudian harga t sama dengan nol, maka akan diperoleh :
Demikian
seterusnya, sehinga apabila Mx(t) diturunkan terhadap t sebanyak r kali, kemudian harga t
sama dengan nol, maka akan diperoleh:
1. Dalam hal ini, kita akan menurunkan
terhadap t dari perumusan pada
definisi 1.
Demikian seterusnya,
sehingga apabila Mx(t)
diturunkan terhadap t sebanyak r kali, kemudian harga t sama dengan nol, maka akan diperoleh :
C. Penurunan Momen Dari Fungsi Pembangkit Momen
Jika X adalah peubah acak, baik diskrit
maupun kontinu dan Mx(t) adalh fungsi pembangkit momennya, maka :
Jika
kita memperhatikna uraian diatas, maka syarat fungsi pembangkit momen akan
menghasilkan momen–momen adalah –h < t
< h dan h > 0. Apa artinya? Coba kita
subsitusikan beberapa nilai h ke
dalam –h < t < h.
Untuk h = ½, akan diperoleh -½ < t < ½
Untuk t =1 ,akan diperoleh -1 <
t < 1
Untuk t = 10, akan diperoleh -10
< t < 10
Untuk t = 25, akan diperoleh -25 < t < 25
Untuk t = 25, akan diperoleh -25 < t < 25
Untuk t = 100, akan diperoleh -100
< t < 100
Untuk t=200, akan diperoleh -200
< t < 200
Maka
kita dapat menyimpulkan bahwa nilai t
itu harus mencakup 0 (nol). Akibatnya, apabila fungsi pembangkit momen menghasilkan
sebuah fungsi t dengan harga t-nya tidak sama dengan nol, maka kita harus
menentukan fungsi pembangkit momen yang berlaku untuk harga t sama dengan nol.
Pemahaman
penentuan fungsi pembangkit momen dari sebuah peubah acak, baik diskri maupun
kontinu diperjelas melalui contoh berikut:
Contoh:
Misalnya
fungsi peluang dari X berbentuk:
a. Tentukam fumgsi pembangkit momen dari X.
b. Hitung μ’1 dan μ’2 berdasarkan hasil fungsi pembangkit
momen.
Penyelesaian:
Berdasarkan
definisi fungsi pembangkit momen diskrit, maka:













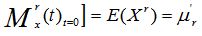







No comments:
Write komentar