Prinsip Dasar Perhitungan dan Kaidah Pencacahan

A. Prinsip Dasar Perhitungan

Ada dua prinsip dasar yang digunakan dalam menghitung yaitu aturan penjumlahan dan aturan perkalian.   

1. Prinsip dasar perhitungan

Jika suatu himpunan A terbagi dalam himpunan bagian A1, A2,...An, maka jumlah unsur pada himpunan A akan sama dengan jumlah semua unsur yang ada pada setiap himpunan bagian A1, A2,...An.

Secara tidak langsung, pada prinsip penjumlahan, setiap himpunan bagian  A1, A2,...An, tidak saling tumpang tindih ( saling lepas ). Untuk himpunan yang saling tumpang tindih tidak berlaku lagi prinsip penjumlahan, dan ini harus diselasaikan dengan prinsip inklusi-ekslusi yang akan dibahas kemudian.

Contoh :

a. Seorang guru SD di daerah, mengajar murid kelas 4, kelas 5, dan kelas 6. Jika jumlah murid kelas 4 adalah 25 orang dan jumlah murid kelas 5 adalah 27 orang serta jumlah murid kelas 6 adalah 20 orang, maka jumlah murid yang diajar guru tersebut adalah 25+27+20= 72 murid

b. Seseorang mahasiswa ingin memebeli sebuah motor. Ia dihadapkan untuk memilih pada setu jenis dari tiga merek motor, honda 3 pilihan, susuki 2 pilihan, dan yamaha 2 pilihan. Dengan demikian, mahasiswa tersebut mempunyai pilihan sebanyak 3+2+2=7 pilihan

2. Prinsip perkalian

Misalkan sebuah prosedur dapat dipecah dalam dua penugasan. Penugasan pertama dapat dilakukan dalam n₁ cara, dan tugas ke dua dapat dilakukan dalam n₂ cara setelah tugas pertama dilakukan. Dengan demikian, dalam mengerjakan prosedur tersebut pada (n₁ x n₂) cara. Secara tidak langsung, pada perinsip perkalian, bisa terjadi saling tumpang tindih (tidak saling lepas).

Contoh :

Seorang guru SD didaerah, mengajar murid kelas 4, kelas 5, dan kelas 6. Jika jumlah murid kelas 4 adalah 25 orang dan jumlah murid kelas 5 adalah 27 orang serta jumlah murid kelas 6 adalah 20 orang, jika guru tersebut ingin memilih tiga orang murid dari anak didiknya, dimana seorang murid dari setiap kelas, maka guru tersebut mempungai 25x27x20=13500 cara dalam memilih susunan 3 murid tersebut

B. Kaidah Pencacahan

Kaidah pencacahan atau Counting Slots  adalah suatu aidah yang digunakan untuk menentukan atau menghitung berapa  banyak cara yang terjadi darisuatu peristiwa.

Kaidah pencacahan terdiri atas:

1. Pengisian tempat yang tersedia (Filling Slots),

2. Permutasi,

3. Kombinasi.

Pengisian Tempat yang Tersedia (Filling Slots)

Jika suatu peristiwa dapat dikerjakan dengan K₁ cara yang berbeda, peritiwa kedua dapat dikerjakan dengan K₂ yang berbeda dan seterusnya sampai peristiwa ke-n, maka banyaknya cara yang berbeda dari semua peristiwa tersebut adalah K, dimana K = K₁ x K₂ x ... ... x K_n.
K disebut dengan istilah banyaknya tempat tempat yang tersedia dengan aturan perkalian atau kaidah perkalian.

Untuk menentukan banyaknya tempat yang gtersedia dapat mengunkanan tabel siang, diagram pohon, dan pasangan berurutan.

Contoh :

Misalkan ada 2 celana berwarna hitam dan biru serta 4 baju berwarna kuning, merah, purih, dan ungu. Ada berapa banyak pasangan warna celana dan baju yang dapat dibentuk ?

Dari contoh kasus di atas, dapat diselesaikan dengan kaidah pencacaha. Banyaknya cara yang mungkin terjadi dari peristiwa tersebut, dapat diketahui dengan meggunakan metode berikut.

1. Diagram Pohon

Diagram pohon merupakan suatu metode yang ditempuh dalam menentukan banyak cara yang terjadi dalam sebuah peristiwa yang biasanya berbentukpohon karena bercabang.

Contoh kasus di atas.

2. Tabel Silang

Metode tabel silang adalah metode yang digunakan dalam menentukan suatu cara dalam sebuah peristiwa yang biasanya disajikan dalam bentuk tabel.

Misalkan dari contoh kasusu di atas, maka penyelesaian dengan metode tabel silang adalah sebagai berikut.

Celana	Baju
	Kuning (K)	Merah (M)	Putih (P)	Ungu (U)
Hitam (H)	HK	HM	HP	HU
Biru (B)	BK	BM	BP	BU

3. Pasangan Berurutan

Pasangan berurutan merupakan suatu cara menuliskan anggota dua himpunan yang dipasangkan, anggota pertama pasangna itu berasal dari himpunan yang pertama dan anggota kedua berasal dari himpunan yang kedua.

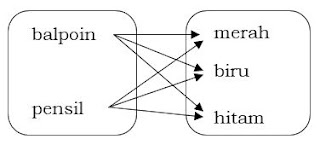
Misalkan A = {Bolpoin, Pensil} dan B = {Merah, Biru, Hitam}. Pasangan berurut A dan B dapat dinyatakan sebagai diagram panah seprti pada gambar

Pada diagram panah diatas dapat disusun pasangan berurutan antara pilihan barang dan pilihan warna sebagai berikut.

( Balpoin, Merah )                         ( Pensil, Merah )

( Balpoin, Biru )                            ( Pensil, Biru )    

( Balpoin, Hitam )                         ( Pensil, Hitam )

Jadi, diperoleh 6 pasang pilihan yang dapat kalian lakukan.