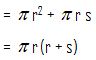Iwan Ridwan: Bangun Ruang Sisi Lengkung

Showing posts with label Bangun Ruang Sisi Lengkung. Show all posts

Saturday, 28 April 2018

Luas Permukaan dan Volume Bola

Bangun Ruang Sisi Lengkung Iwan Ridwan April 28, 2018

A. Unsur-unsur Bola

Bola merupakan bangun ruang sisi lengkung yang dibatasi oleh satu bidang lengkung yang tidak memiliki rusuk. Bola dapat dibentuk dari bangun setengah lingkaran yang diputar sejauh 360⁰ pada garis tengahnya. Unsur-unsur bola sebagai berikut.

a. Titik O adalah titik pusat

b. Garis AB adalah diameter bola

c. Garis OA dan OB adalah jari jari bola

B. Luas Permukaan Bola

Luas permukaan bola adalah sebagai berikut.

Dimana:

L = luas permukaan bola

r = jari-jari bola

C. Volume Bola

Rumus volume bola adalah sebagai berikut.

Dimana:

V = volume bola

r = jari-jari bola

D. Contoh Soal

1. Jari-jari sebuah bola adalah 10 cm. Hitunglah luas permukaan bola tersebut!

Penyelesaian

Diketahui:

r = 10 cm

Ditanyakan:

L _{permukaan b}_ola = . . . .

Solusi

= 4 × 3,14 × 10²

= 4 × 3,14 × 100

= 4 × 314

= 1256 cm²

2. Iwan memegang sebuah bola yang memiliki jari-jari 15 cm. Hitunglah volume bola yang dipegang oleh Iwan!

Penyelesaian

Diketahui:

r = 15 cm

Ditanyakan:

V _bola = . . . .

Solusi

= 4 × 3,14 × 5 × 15 × 15

= 14130 cm³

3. Sebuah bola memiliki volume 14130 cm³. Hitunglah luas permukaan bola tersebut!

Penyelesaian

Diketahui:

V = 14130 cm³

Ditanyakan:

L _{permukaan bola} = . . . .

Solusi

14130 = × 3,14 × r³

14130 = × r³

14130 × 3 = 12,56 × r³

42390 = 12,56 × r³

r³ = 3375

r = 15 cm

Luas permukaan Bola

= 4 × 3,14 × 15²

= 12,56 × 225

= 2826 cm²

Jadi luas permukaan bola adalah 2826 cm²

4. Kubah sebuah mesjid berbentuk setengah bola dengan diameter 14 meter. Kubah tersebut terbuat dari Aluminium. Jika 1 m² Aluminium harganya adalah Rp. 30.000,-. Hitunglah biaya pembuatan kubah mesjid tersebut.

Penyelesaian

Diketahui:

D = 14 m

Harga (H) = Rp. 30.000,-/m²

Luas kubah = ½ luas permukaan bola

Ditanyakan:

Biaya (B) = . . . .

Solusi

Luas kubah = ½ luas permukaan bola

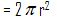
= 44 × 7

= 308 m²

Untuk menentukan biaya dapat diselesaikan dengan cara berikut

Biaya (B) = Harga (H) × Luas kubah (L)

B = H × L

= 30000 × 308

= 9240000

Jadi biaya yang diperlukan untuk membuat kubah mesjid adalah Rp. 9.240.000,-

Wednesday, 25 April 2018

Luas Permukaan dan Volume Kerucut

Bangun Ruang Sisi Lengkung Iwan Ridwan April 25, 2018

A. Unsur-unsur Kerucut

Kerucut merupakan bangun ruang sisi lengkung yang menyerupai limas segi beraturan yang bidang alasnya berbentuk lingkaran. Unsur-unsur kerucut sebagai berikut.

a. Bidang Alas

b. Selimut Kerucut

c. Tinggi Kerucut

d. Diameter Alas Kerucut

e. Jari-jari Alas Kerucut

f. Garis Pelukis

B. Jaring-jaring Kerucut

C. Luas Permukaan Kerucut

Luas permukaan kerucut dapat dicari dengan cara mencari luas masing-masing bagian kerucut kemudian dijumlahkan. Sebelum mencari luas permukaan kerucut yang pertama yang harus kita cari terlebih dahulu adalah mencari rumus luas selimut kerucut. Perhatikan gambar jaring-jaring kerucut di atas. Panjang busur pada juring sama dengan keliling lingkaran alas kerucut. Untuk mencari luas selimut kerucut, bandingkan luas juring dengan luas lingkaran yang berpusat di titik C yang jari-jarinya sama panjang dengan garis pelukis kerucut yaitu s sehingga diperoleh:

Jadi luas selimut kerucut adalah:

Jadi, luas selimut kerucut adalah

Setelah mengetahui rumus selimut kerucut selanjutnya kita mencari rumus luas permukaan kerucut. Luas permukaan kerucut dapat kita cari dengan menjumlahkan luas bagian-bagian kerucut yaitu luas alas kerucut yang berbentuk lingkaran dengan luas selimut kerucut sehingga diperoleh:

Luas permukaan kerucut = luas alas kerucut + luas selimut kerucut

Jadi rumus luas permukaan kerucut adalah:

atau

Dimana:

r = jari-jari alas kerucut

s = garis pelukis kerucut

D. Volume Kerucut

Keucut dapat dipandang sebagai limas tegak yang bidang alasnya berbentuk lingkaran. Jadi rumus volume kerucut dapat dicari dengan menggunakan rumus limas dan dinyatakan sebagai berikut:

Karena alas kerucut berbentuk lingkaran maka rumus vlume kerucut dapat ditulis

Jadi rumus volume kerucut adalah:

Dimana:

r = jari-jari alas kerucut

t = tinggi kerucut

atau

E. Contoh Soal

1. Sebuah kerucut mempunyai jari-jari alas 7 cm dan tinggi 24 cm. Hitunglah!

a. Panjang garis pelukisnya

b. Luas selimut kerucut

b. luas permukaan kerucut

Penyelesaian:

Kita misalkan bahwa garis pelukis kerucut tersebut adalah s

Diketahui:

r = 14 cm

t = 48 cm

Ditanyakan:

a. s = . . . .

b. L_{selimut kerucut} = . . . .

c. L _{permukaan kerucut}= . . . .

Solusi

a. s² = r² + t²

= 7² + 24²

= 49 + 576

= 625

s =

= 25 cm

Jadi, panjang garis pelukisnya adalah 25 cm.

= 550 cm²

= 22 × 32

= 704 cm²

2. Sebuah kerucut mempunyai panjang jari-jari alas 15 cm dan panjang garis pelukis 17 cm. Hitunglah volume kerucut tersebut!

Penyelesaian:

Diketahui:

r = 15 cm

s = 17 cm

Ditanyakan:

V _kerucut = . . . .

Solusi

V _kerucut=

Karena t belum diketahui maka kita mencari nilai t terlebih dahulu menggunakan teorema Pythagoras

t² = s² – r²

= 17² - 15²

= 289 - 225

= 64

= 8 cm

= 4003,5 cm³

Sunday, 22 April 2018

Luas Permukaan dan Volume Tabung

Bangun Ruang Sisi Lengkung Iwan Ridwan April 22, 2018

Tabung

A. Unsur-unsur Tabung

Tabung merupakan bangun sisi lengkung yang memiliki bidang alas dan bidang atas (tutup) berbentuk lingkaran yang sejajar dan kongruen, serta bidang samping yang disebut selimut tabung yang berbentuk persegi panjang. Unsur-unsur tabung sebagai berikut.

1. Sisi alas dan sisi atas (tutup).

2. Selimut tabung

3. Tinggi tabung

4. Diameter tabung

5. Jari-jari tabung

B. Jaring-jaring Tabung

C. Luas Permukaan Tabung

Luas permukaan tabung dapat dicari dengan cara mencari luas masing-masing bagian tabung.

Luas permukaan tabung = luas alas tabung + luas atas (tutup) tabung + luas selimut tabung
= 2 × luas alas tabung + (keliling alas tabung × tinggi tabung)